«Ваш кофе стоит четыре тысячи»: игра и математика в детском саду

Игра является важнейшим условием развития детей дошкольного возраста, но образовательные задачи, в том числе развитие математических представлений, никто не отменял. Многим родителям хочется, чтобы их ребенок, с одной стороны, наигрался в детском саду, а с другой — умел хорошо считать к школе. Педагоги пытаются найти баланс, но часто это приводит к парадоксальным результатам: игра исчезает из детских садов, а интерес к математике так и не появляется.

Почему это происходит? Важна ли спонтанная игра для развития математических представлений? Возможно ли интегрировать игру и обучение так, чтобы детская игра не разрушалась? На эти вопросы с опорой на научные исследования ответили сотрудники лаборатории развития ребенка НИИ урбанистики и глобального образования МГПУ Анна Якшина и Екатерина Стародубцева.

Когда происходит первая встреча ребенка с математикой и математическим образованием

Математическое развитие ребенка начинается задолго до того, как он впервые сталкивается с организованным обучением. Сравнения, классификации, ритмы, формы и числа — всё это ребенок исследует в повседневной жизни с раннего возраста.

Первичный опыт важен, но спонтанные встречи с математическими феноменами еще не являются математическим образованием — ведь оно предполагает осознание смысла явлений и ситуаций, способность задавать вопросы или объяснять свое понимание, используя математический язык.

Первичный опыт превращается в настоящее математическое образование во взаимодействии ребенка со взрослым. Именно от взрослого во многом зависит, поддержит ли математика естественное детское любопытство к миру, или окажется сложной и формализованной системой, далекой от личного опыта ребенка.

Как представление взрослых о математике влияет на детский опыт

Чтобы разобраться в этой теме, важно самим ответить на несколько простых вопросов.

• Как вы воспринимаете математику: это увлекательный мир открытий или скучная и сложная дисциплина?
• Что для вас значит «изучать математику»: осваивать ее техническую сторону (способы вычислений, измерений и пр.) или исследовать и решать реальные задачи?
• Что для вас важнее в математике: правильные ответы и алгоритмы или аргументация, размышления и поиск решений?

От ответов педагогов на эти вопросы будут зависеть и стиль обучения, и отношение детей к математике, и то, как именно будет устроен образовательный процесс в детском саду, в том числе — будет ли в нем место для свободной деятельности и игры.

«То, как мы видим детей и что думаем о них, влияет на то, как мы их учим. Если мы убеждены, что у ребенка нет никаких математических представлений, обучение будет похоже на заполнение пустого сосуда. Если же мы понимаем и признаем, что дети с первых дней жизни осваивают и исследуют мир во всей его полноте, включая математические феномены, а к дошкольному возрасту у детей уже сформировано множество личных математических концепций, — обучение, скорее, будет уважительным к имеющимся у детей знаниям и идеям, а взрослые смогут с интересом наблюдать и слушать детей, чтобы помогать им расширять и обогащать представления».

Мэрилин Флир
Early learning and development: cultural-historical concepts in play

В начале 2010-х годов исследователь в сфере раннего математического образования Э. Каррутерс предложила использовать термин «открытая математика» для обозначения подхода к математическому образованию, чуткого и бережного к собственной математике детей, к их идеям, гипотезам, экспериментам и стратегиям. «Открытая математика» нацелена на создание культуры математических исследований, на поддержку и взращивание мышления, на уточнение и поиск математических идей, проявляющихся в повседневной деятельности, инициированной самими детьми. Такой подход не ограничивается набором разрозненных видов деятельности, не противопоставляет математику и свободную деятельность и игру, а наоборот, позволяет педагогу создать такие условия в дошкольной группе, в которых все виды деятельности будут усиливать друг друга.

Как обстоят дела с математическим образованием дошкольников на практике

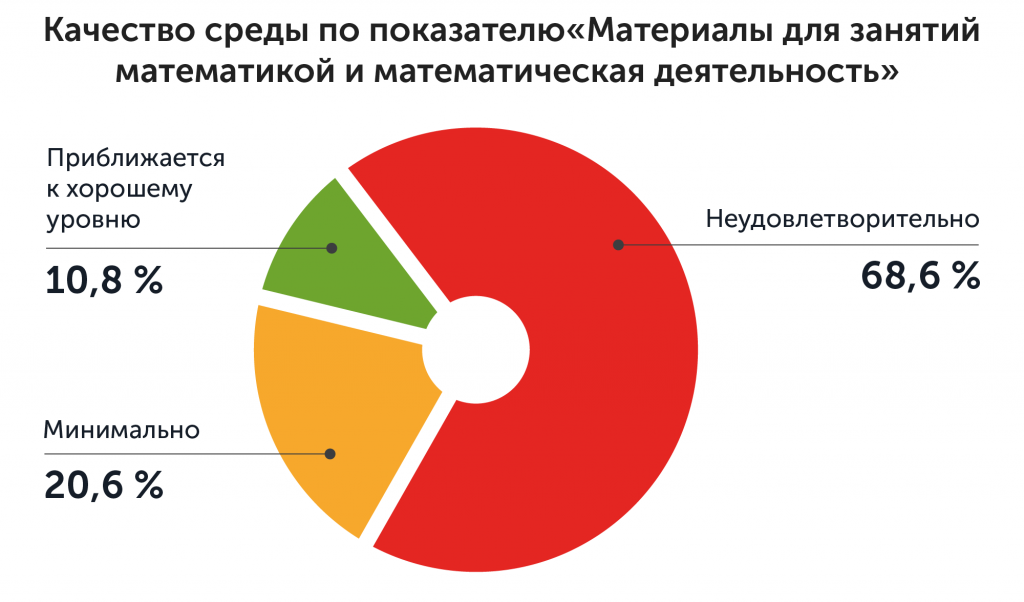
Исследования качества образовательной среды, проведенные сотрудниками Лаборатории развития ребенка в российских дошкольных группах с использованием шкал ECERS-3, показывают, что оценку «неудовлетворительно» по показателю «Материалы для занятий математикой и математическая деятельность» получили более 60 % дошкольных групп. К хорошему уровню приближаются лишь около 11 % групп.

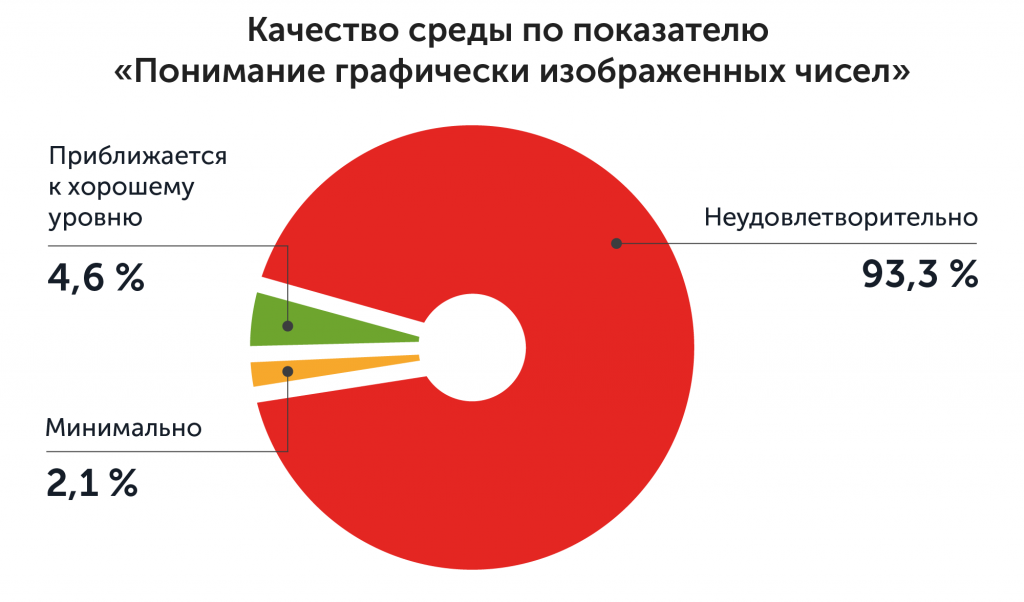
Еще хуже обстоят дела с материалами и взаимодействием, которые помогают детям понимать, что означают записанные числа (то есть как соотносятся числовая запись и количество предметов): оценку «неудовлетворительно» по показателю «Понимание графически изображенных чисел» получили более 90 % групп.

Для математического развития важно, чтобы и во время свободной деятельности, и во время организованного обучения детям была доступна богатая математическая среда. Это очевидная общепризнанная идея, поэтому в каждой дошкольной группе без труда можно найти «математический уголок» или даже центр математики — пространство, в котором на низких открытых стеллажах и полках размещены материалы для занятий математикой. Однако часто эти пространства пустуют, дети во время свободной деятельности не подходят к стеллажам, материалы не разнообразны и не вызывают интереса у дошкольников.

Также можно обнаружить, что в обычной практике дошкольных групп образовательный процесс понимается и реализуется как организованные занятия по расписанию, где музыка сменяет развитие речи, формирование элементарных математических представлений или обучение грамоте. Е. Е. Кравцова пишет, что еще Л. С. Выготский предупреждал об опасности превращения детских садов в «маленькие школы», и всё же это произошло: фронтальные занятия школьного типа стали занимать слишком много времени, появляются аналоги школьных отметок, а взрослые все чаще общаются с детьми как учителя с учениками.

Какие еще дефициты фронтальных занятий можно выявить при наблюдении:

• не оставляют места обсуждению проблематизирующих вопросов, дискуссии, построению гипотез и обмену идеями;
• редко бывают нацелены на то, чтобы обнаружить, как дети сами понимают математические феномены и концепции;
• обращены к предполагаемому «среднему уровню» математического развития и не обеспечивают эффективную поддержку тем, кто испытывает трудности, или, наоборот, готов к освоению более сложных математических идей.

Подобное обучение математике по образцу школьных занятий приводит совсем не к тем результатам, которых ожидают педагоги и родители. Многие исследования показывают, как к началу школьного обучения естественный интерес к математике сменяется неприязнью, неуверенностью или даже страхом. Педагогам нужны инструменты, позволяющие одновременно обучать детей математике с опорой на их собственный смысл и интересы, и соблюдать баланс свободной и организованной деятельности для поддержки детской инициативности.

Как обучать математике с опорой на детские интересы

Некоторые исследователи считают, что хотя дети усваивают множество математических идей в процессе повседневной свободной деятельности, все же этого недостаточно, поскольку дети не учатся математизировать — то есть интерпретировать и осмыслять свой опыт в математической форме.

Это означает, что для дошкольников важен баланс обеих составляющих: свободной деятельности, в которой дети получают неформальный первичный математический опыт и проявляют свое понимание математических идей, и целенаправленно организованного обучения. При этом важно находить и использовать такие формы обучения, которые психологически адекватны возрасту и отвечают интересам дошкольников. В российской и мировой практике дошкольного образования мы можем встретить большое разнообразие таких форм, например:

• взаимодействие с детьми в центре математики во время организованной работы в центрах активности;
• индивидуальные и групповые презентации способов работы с математическими материалами (практика детских садов Монтессори);
• образовательные провокации (практика Реджио-педагогики);
• математические и естественно-научные проекты;
• совместные математические игры;
• дискуссии, обсуждение математических идей и проблем, которые обнаруживаются в ходе повседневной жизни детей в детском саду.

Есть множество неигровых способов обучения математике. При этом спонтанная игра — важная часть жизни дошкольников.

Современные исследователи утверждают: важно не разделять игру и обучение, а наоборот — стараться соединять их так, чтобы они усиливали друг друга.

Совместимы ли математика, требующая точности, и спонтанная игра, где все понарошку

В игре ребенок создает воображаемую ситуацию, использует предметы-заместители: например, ручку или палочку как градусник. Игровые действия условны, что способствует развитию воображения и формированию знаковой функции сознания, без которых в дальнейшем невозможно понимание и оперирование абстрактными математическими символами. Целый ряд исследований показывает важность игры с кубиками и другими неструктурированными материалами для развития пространственных представлений и понимания математики. Есть данные, свидетельствующие о том, что количество времени на спонтанную игру положительно связано с уровнем развития математических навыков детей 5 лет.

Однако если понаблюдать за спонтанной игрой детей дома или в детском саду, то можно услышать, как дети используют, например, счет или измерения. При этом все происходит в игровом контексте, дети считают условно, «как будто», и часто это настораживает наблюдающего взрослого: не закрепится ли неправильное понимание? Не вредит ли такая игра обучению математике?

На примере одного игрового эпизода попробуем разобраться, есть ли место математике в детской игре.

На первый взгляд, очевидно, что ребенок считает неправильно и называет покупателю неправдоподобно высокую цену за стаканчик кофе, перемножая случайные числа, т. е. ребенок не умеет считать. Стоит ли в такой ситуации поправить ребенка и объяснить, какие вычисления будут правильными?

Д. Б. Эльконин отмечал, что «игра не есть упражнение», ее содержанием являются социальные отношения. В одном из своих экспериментов он пытался научить детей использовать мерку во время игры в магазин и просил ребенка отрезать нужное количество ткани. Ребенок же в роли продавца как будто отрезал и передавал ткань покупателю, продолжая игру дальше.

Как и в нашем примере, играющему ребенку была важна не реалистичность, а игровой смысл ситуации и отношения покупатель-продавец. Ребенок в игре действует всегда условно, попытка же добиться правильного ответа выведет его в реальное поле и разрушит игру.

Правильное выполнение математических операций — это только операциональная сторона вопроса, она, безусловно, тоже важна, но в игре развивается не она. Международная программа по оценке образовательных достижений учащихся PISA рассматривает функциональную грамотность как способность применять полученные знания и навыки для решения жизненных задач в разных сферах. Результаты PISA в России показывают, что школьники хорошо решают задачи, но плохо соотносят знания и реальность. И здесь игра вносит значительный вклад в осмысление разных ситуаций, в которых нужна математика.

Если присмотреться к описанному эпизоду и заглянуть глубже, то мы увидим, что ребенок переносит в игру свой опыт обращения со счетом в повседневных ситуациях:

• чтобы купить кофе, нужно понимать, сколько он стоит;
• для счета можно использовать кассовый аппарат;
• есть операция умножения;
• есть разные порядки чисел (десятки, сотни, тысячи) и т. д.

Иными словами, в игре отразился интерес ребенка и его понимание смысловой стороны счета: зачем вообще нужно что-то считать.

Что говорят исследователи: спонтанная игра как пространство детского смысла

Б. ван Урс подчеркивает, что развитие математического мышления начинается именно с участия ребенка в коммуникативных культурных практиках, имеющих для него смысл. Возможность играть и осмыслять свой опыт через игру является важным условием подлинного обучения математике.

М. Уортингтон в своем исследовании показывает, что если у детей есть богатая математическая среда дома и в детском саду, то в совместной игре без участия взрослого дети осмысляют свои «культурные знания» о математике и активно используют счет, говорят о времени, упоминают формы, делают измерения, сравнивают больше – меньше, используют такие понятия, как вес, скорость, температура, работают с данными и т. д. Кроме того, дети активно используют математические обозначения (стрелки, цифры, символы) во время игровой коммуникации.

Э. Зипперт с коллегами отмечают, что важен изначальный уровень математических представлений детей, включающихся в совместную игру: чем он выше, тем больше дети вербально и невербально обращаются к математике во время игры, т. е. в игре без участия педагога происходит опробование уже освоенного содержания и математических навыков, дети также обсуждают математические понятия друг с другом.

М. Уортингтон отмечает, что наблюдательному взрослому свободная спонтанная деятельность детей может «рассказать» многое об интересах детей и особенностях их мышления, о том, как они понимают и используют математические идеи и символы, какой следующий шаг в математическом развитии могут сделать. Такие наблюдения помогают педагогам увидеть математику из детской перспективы и выстраивать образовательный процесс в зоне ближайшего развития. Таким образом, для оптимального обучения математике важно, чтобы в дошкольной группе одновременно была и богатая математическая среда, и возможности для развития спонтанной игры без привнесения в нее дидактических задач извне.

^{Авторы текста:
Анна Якшина, научный сотрудник лаборатории развития ребенка НИИ урбанистики и глобального образования МГПУ
Екатерина Стародубцева, специалист лаборатории развития ребенка НИИ урбанистики и глобального образования МГПУ
Редактор: Татьяна Сандакова
_{Фото: Детский сад N 56 г. Кострома}}